

In an atom, the electronic space is divided into shells. The three quantum numbers mentioned in the section above are used to identify an orbital in an atom. Quantum numbersĪn atom can have a large number of orbitals. Finally, the magnetic quantum number m is a set of integers from − l to l m = − l, −( l − 1) … −1, 0, 1 … ( l − 1), l. The principal quantum number n is a set of positive integers n = 1, 2, 3… The azimuthal quantum number l is a set of non-negative integers ranging from 0 to ( n − 1) l = 0, 1, 2 … ( n − 2), ( n − 1). Hence, we can conclude these three quantum numbers represent an orbital. For each set of these three quantum numbers, we get a new wave function. N − l − 1 is a generalized Laguerre polynomial.Īs you can see from the above, the quantum numbers n, l, and m decide the equation of the wave function Ψ. Here, a 0 is the Bohr radius,, and L 2 l + 1 Here, n, l, and m are the principal, azimuthal, and magnetic quantum number. L( θ, ϕ) is spherical harmonics, which determine the direction of the orbital. R( r) is the radial function, which decides the nuclear distance while Y m The wave function for the hydrogen atom in the spherical coordinate system is as follows: The hydrogen atom has only one electron and only atom for which the Schrodinger equation can be solved exactly. The atomic orbital is the region with a 90 % probability. Practically, we define the orbital based on the probability of 90 %, not 100 %. Thus, the size of the orbital, when the probability of finding an electron is 100 %, is equal to the size of the universe, i.e. The probability of an electron at the position x between a and b is given by the equation below.
|Ψ| 2 represents the probability density function. It provides the probability distribution of an electron and is denoted by Ψ. In quantum mechanics, a wave function is a complex mathematical description of a quantum state. Thus, an orbital is an electronic probabilistic cloud around the nucleus. The probability of finding the electron in this region is high (say 90 %), and the electron might exist beyond it.

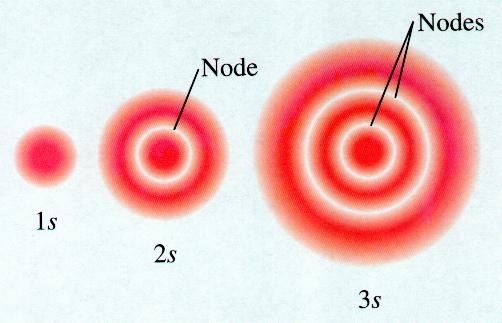
The region surrounding the nucleus is the probabilistic region, not discrete. 1s orbital is the simplest and lowest energy orbital. The nucleus is at the center of the orbital, and the electron revolves around the nucleus. The simplest orbital of all is 1s orbital, which is spherical in shape (see figure below). A better way to define the atomic orbital is the space around the nucleus which has a high probability of finding the electron. The atomic orbital is a complex mathematical function called a wave function, which decides the energy, angular momentum, and location of an electron.


 0 kommentar(er)
0 kommentar(er)
